Hasil bayangan suatu objek oleh rotasi dipengaruhi jauh besar sudut, arah, dan letak titik pusat rotasi. Besar sudut rotasi dinyatakan dalam bilangan dengan satuan derajat (αo). Arah rotasi yang searah jarum jam ditandai dengan simbol tanda negatif di depan besar sudut rotasi. Misalnya, suatu objek mengalami transformasi rotasi searah jarum jam dengan besar sudut 45o dengan pusat P(a, b). Transformasi rotasi untuk objek tersebut dapat dinyatakan dalam tanda rotasi R[P(a, b), –45o]. Cara menentukan bayangan objek oleh rotasi searah jarum jam dapat melalui sebuah persamaan umum.
Sebuah titik yang dirotasikan dengan pusat dan arah tertentu akan berpindah letak koordinatnya. Perpindahan letak titik koordinat memenuhi persamaan yang dipengaruhi besar sudut rotasi, arah rotasi, dan letak titik pusat rotasi. Rotasi pada transformasi geometri dapat dilakukan pada objek berupa titik, garis, bangun datar, dan lain sebagainya. Rotasi untuk sebuah objek berupa garis atau bidang dilakukan dengan cara merotasikan setiap titik pada garis atau bidang tersebut. Contoh rotasi suatu objek sejauh 90odengan arah searah jarum jam diberikan seperti gambar di bawah.
Bagaimana cara menentukan hasil bayangan suatu objek oleh rotasi searah jarum jam? Sobat idshool dapat mencari tahu lebih banyak melalui ulasan rotasi berlawanan arah jarum jam (α = 30o, 45o, 60o, 90o, 180o) di bawah.
Baca Juga: Transformasi Geometri – Translasi, Refleksi, Dilatasi, dan Rotasi
Rotasi Searah Jarum Jam pada Pusat O(0, 0) Sejauh αo : R[O(0, 0), –αo]
Hasil rotasi titik dapat dicari dengan alat bantu seperti jangka dan busur derajat. Namun, cara tersebut tentu akan memakan waktu lama dan tidak efektif. Sehingga dibutuhkan cara yang lebih baik untuk mendapatkan hasil rotasi suatu obyek. Cara yang lebih baik dapat dilakukan melalui persamaan umum untuk mendapatkan hasil rotasi searah jarum jam. Persamaan tersebut diperoleh dengan mencari hubungan antara titik awal dan titik hasil rotasi. Hubungan kedua titik dapat dibentuk melalui fungsi trigonometri.
Secara umum, hasil rotasi dengan pusat O(0, 0) sejauh αo searah jarum jam atau R[P(a, b), –αo] dapat diperoleh melalui matriks transformasi berikut.
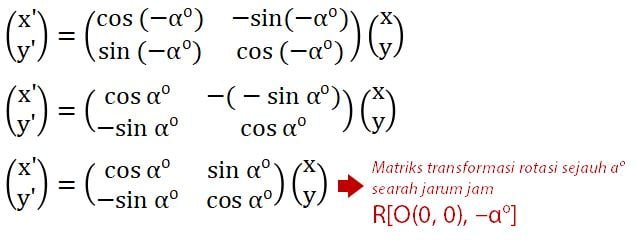
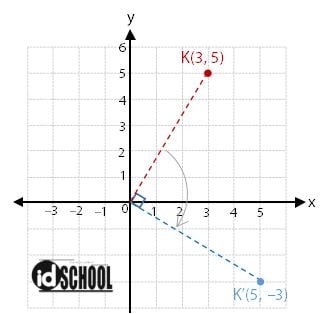
Sebagai contoh, rotasi titik A(x, y) pada pusat O(0, 0) sejauh 90o searah jarum jam akan menghasilkan titik A’(x’, y’). Di mana, letak titik koordinat (x’, y’) memenuhi persamaan berikut.
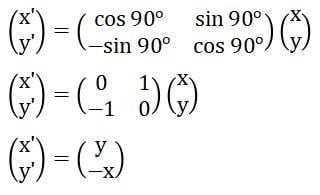
Jadi, hasil transformasi titik A(x, y) sejauh 90o searah jarum jam adalah titik A’(y, –x). Contoh: rotasi titik K(3, 5) sejauh 90o searah jarum jam adalah titik K’(5, –3).
Selanjutya, dengan cara yang sama dapat diperoleh persamaan umum untuk mendapatkan hasil rotasi pada pusat O(0, 0) dengan besar sudut rotasi α = 30o, 45o, 60o, 180o, 270o dan besar sudut lainnya. Ringkasan persamaan umum hasil rotasi titik (x, y) pada pusat O(0, 0) dengan besar sudut rotasi α = 30o, 45o, 60o, 90, 180o, dan 270o diberikan seperti tabel berikut.

Baca Juga: Mengenali Bentuk Perbedaan Barisan Aritmatikan dan Geometri
Rotasi Searah Jarum Jam pada Pusat P(a, b) Sejauh αo : R[P(a, b), –αo]
Cara melakukan rotasi searah jarum jam pada pusat P(a, b) sama seperti cara melakukan rotasi searah jarum pada pusat O(0, 0). Perbedaan dari keduanya hanya terlatak pada titik pusat yang menjadi tumpuan rotasi. Secara umum, hasil rotasi dengan pusat P(a, b) sejauht αo yang searah jarum jam atau R[P(a, b), –αo] dapat diperoleh melalui matriks transformasi berikut.

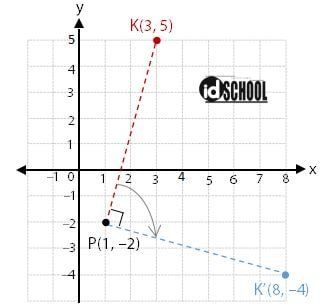
Sebagai contoh, rotasi titik A(x, y) pada pusat P(a, b) sejauh 90o dengan arah searah jarum jam akan menghasilkan titik A’(x’, y’). Di mana (x’, y’) memenuhi persamaan berikut.
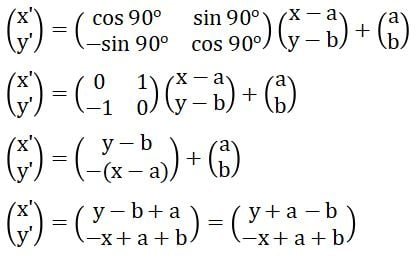
Jadi, hasil transformasi titik A(x, y) sejauh 90o yang searah jarum jam adalah titik A’(y + a – b, –x+ a + b). Contoh: rotasi titik K(3, 5) pada pusat P(1,−2) sejauh 90o searah jarum jam adalah titik K’(5 + 1 −(−2), −3 + 1 + (−2)) = K’(8, −4).
Selanjutya, dengan cara yang sama dapat diperoleh persamaan umum untuk mendapatkan hasil rotasi pada pusat P(a, b) dengan besar sudut rotasi α = 30o, 45o, 60o, 180o, 270o dan besar sudut lainnya. Secara ringkas, persamaan umum hasil rotasi titik (x, y) pada pusat P(a, b) dengan besar sudut rotasi α = 30o, 45o, 60o, 90, 180o, dan 270o diberikan seperti tabel berikut.
Baca Juga: Komposisi Matriks Transformasi Geometri
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman terkait bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan dalam mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Rotasi Sejauh αo Searah Jarum Jam
Titik E (–1, –2) dirotasikan sebesar 90° searah jarum jam terhadap titik (–3, 2). Hasilnya dirotasikan lagi sebesar 180° dengan arah yang sama terhadap titik pusat (–3, 2). Hasil akhir rotasi titik E adalah ….
A. (–7, 0)
B. (0, –4)
C. (1, 4)
D. (4, 1)
E. (7, –4)
Pembahasan:
Rotasi titik E (–1, –2) sebesar 90° searah jarum jam terhadap titik (–3, 2): R[P(–3, 2), –90o]
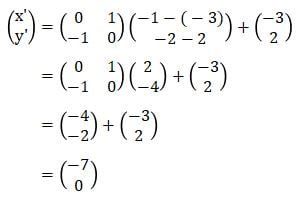
Hasil dari rotasi titik E (–1, –2) dengan R[P(–3, 2), –90o] adalah titik E’(–6, 0). Selanjutnya, titik E’(–6, 0) dirotasikan sebesar 180° dengan arah yang sama terhadap titik pusat (–3, 2).
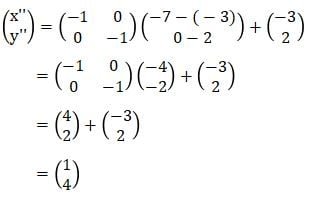
Jadi, hasil akhir rotasi titik E (–1, –2) dirotasikan sebesar 90° searah jarum jam terhadap titik (–3, 2) dan dirotasikan lagi sebesar 180° dengan arah yang sama terhadap titik pusat (–3, 2) adalah titik E’’(1, 4).
Jawaban: C
Baca Juga: Rumus Rotasi Berlawanan Arah Jarum Jam
Contoh 2 – Soal Rotasi Sejauh αo Searah Jarum Jam

Pembahasan:
Hasil rotasi titik (x, y) yang dirotasikan 45o searah jarum jam dengan pusat rotasi titik asal O(0,0) memenuhi persamaan berikut.
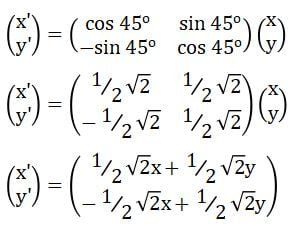
Diperoleh dua persamaan letak titik hasil rotasi:
- Persamaan 1: x’ = 1/2√2x + 1/2√2y
- Persamaan 2: y’ = –1/2√2x + 1/2√2y
Kurangkan persamaan 1 dan persamaan 2 untuk mendapatkan persamaan x’:
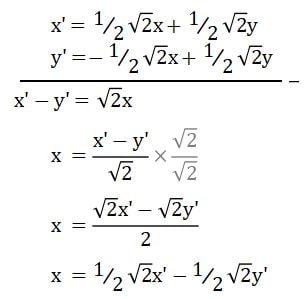
Jumlahkan persamaan 1 dan persamaan 2 untuk mendapatkan persamaan y’:
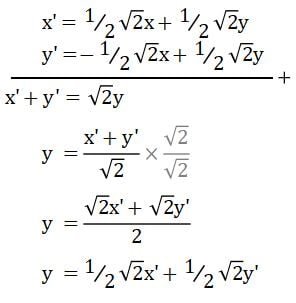
Substitusi nilai x dan y pada persamaan garis ℓ: x + 2y = 4 untuk mendapatkan persamaan garis g yang merupakan persamaan garis hasil rotasi.
x + 2y = 4
1/2√2x’ – 1/2√2y’ + 2(1/2√2x’ + 1/2√2y’) = 4
1/2√2x’ – 1/2√2y’ + √2x’ + √2y’ = 4
3/2√2x’ + 1/2√2y’ = 4
3√2x’ + √2y’ = 8
Diperoleh persamaan garis g: 3√2x’ + √2y’ = 8 sehingga nilai a = 3√2, b = √2, dan c = 8. Jadi, nilai a + b + c = 3√2 + √2 + 8 = 8 + 4√2.
Jawaban: A
Demikianlah tadi ulasan rotasi searah jam sejauh α = 30, 60, 90, 180, dan 270 derajat pada pusat O(0, 0) dan P(a, b). Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menentukan Vektor yang Saling Sejajar dan Vektor yang Saling Tegak Lurus
Sumber gini.com


EmoticonEmoticon