Benda yang bergerak dengan lintasan berbentuk lingkaran dan suatu kecepatan disebut mengalami Gerak Melingkar. Jika kecepatan benda tetap atau konstan maka benda mengalami Gerak Melingkar Beraturan (GMB). Sedangkan pada gerak benda melingkar dengan kecepatan berubah-ubah secara teratur disebut Gerak Melinngkar Berubah Beraturan (GMBB). Setiap benda yang bergerak melingkar memiliki dua kecepatan yaitu kecepatan linear dan kecepatan anguler. Kecepatan gerak benda tersebut dapat diketahui melalui rumus kecepatan linear dan anguler pada gerak melingkar. Kedua kecepatan pada gerak melingkar yaitu kecepatan linear dan kecepatan anguler memiliki pengertian yang berbeda. Namun kedua jenis kecepatan tersebut sama-sama memliki peran penting dalam proses gerak melingkar.
Bayangkan sebuah benda bermassa m diikat pada sebuah tali dengan panjang talinya adalah r. Benda dan tali tersebut kemudian diayunkan terus menerus sehingga tali dalam keadaan tegang dan benda bermassa m berputar melingkar. Lintasan yang dilalui benda tersebut berbentuk lingkaran, sehingga dapat dikatakan bahwa benda mengalami gerak melingkar. Contoh lain gerak melingkar terdapat pada roda yang berputar, komedi putar, gerak planet mengelilingi matahari, dan lain sebagainya.
Apa itu keceparan linear? Apa itu kecepatan anguler pada gerak melingkar? Bagaimana cara mengetahui besar kecepatan linear dan kecepatan anguler pada gerak melingkar? Sobat idschool dapat mencari tahu jawabannya melalui ulsan di bawah.
Baca Juga: Kelajuan dan Kecepatan Sesasat
Kecepatan Linear pada Gerak Melingkar
Kecepatan linear atau kecepatan tangensial pada gerak melingkar adalah kecepatan benda ketika bergerak melingkar dengan arah menyinggung lintasan putarannya. Untuk memperjelas, perhatikan sebuah titik yang terletak pada roda dengan gerak melingkar. Titik tersebut terletak pada titik A pada saat t0 = 0, setelah bergerak selama t sekon titik A berpindah ke titik A’. Jarak tempuh dari A ke A’ merupakan panjang busur S.
Laju yang ditempuh sepanjang panjang busur S selama selang waktu t adalah yang disebut sebagai kecepatan linear/kecepatan tangensial.
Kecepatan linear dalam gerak melingkar menyatakan kecepatan benda untuk berputar satu putaran penuh (per periode). Panjang lintasan yang dilalui dalam gerak melingkar sama dengan keliling lingkaran (KO = 2πr). Sehingga, besar kecepatan linear untuk berputar satu kali putaran penuh atau satu periode dinyatakan dalam persaaamn v berikut.
Baca Juga: Perbedaan Kelajuan dan Kecepatan dalam Bahasan Fisika
Kecepatan Anguler (Kecepatan Sudut) pada Gerak Melingkar
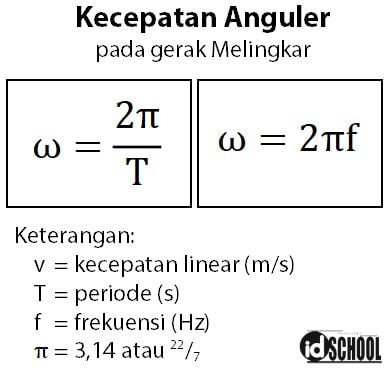
Kecepatan anguler disebut juga dengan kecepatan sudut yang dinyatakan dalam simbol omega (ω). Satuan yang digunakan untuk menyatakan kecepatan sudut adalah rad/s. Di mana rad atau radian menyatakan sebuah satuan untuk besar sudut dengan nilai 360o = 2π radian.
Benda yang bergerak pada lintasannya akan membentuk sudut tertentu dari posisi awal benda diam. Perubahan sudut ini mengikuti arah gerak benda pada lintasan tersebut. Perubahan sudut gerak benda akan bernilai positif jika gerak benda berlawanan dengan arah putaran jam. Adapun perubahan sudut akan bernilai negatif jika arah gerak benda searah dengan arah putaran jam. Besarnya perubahan sudut (Δθ) dalam selang waktu (Δt) tertentu disebut kelajuan anguler.
Untuk mempermudah pemahaman tentang kecepatan anguler, perhatikan kembali sebuah titik pada sebuah roda dengan gerak melingkar. Pada awalnya, titik tersebut terletak pada titik A, kemudian benda menempuh sudut θ setelah bergerak selama t sekon. Perubahan sudut yang ditempuh pada selang waktu t sekon ini yang disebut kecepatan sudut (ω).
Kecepatan sudut pada gerak melingkar menyatakan kecepatan untuk menempuh satu putaran penuh. Besar sudut yang dalam sebuah lingkaran adalah 360o atau sama dengan 2π radian (π rad = 180o). Sehingga, besar kelajuan anguler atau kelajuan sudut dapat diketahui melalui persamaan berikut.
Baca Juga: 4 Metode Penjumlahan Vektor
Contoh Soal Kecepatan Linear dan Anguler (+Pembahasan)
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan disertai dengan pembahasan. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Analisis Pernyataan yang Benar Sesuai Rumus Kecepatan Linear dan Anguler pada Gerak Melingkar
Perhatikan pernyataanpernyataan tentang gerak melingkar beraturan berikut!
(1) kecepatan sudut sebanding dengan frekuensi
(2) kecepatan linear sebanding dengan kecepatan sudut
(3) kecepatan sudut sebanding dengan periode
Pernyataan yang benar adalah nomor ….
A. (1)
B. (1) dan (2)
C. (2)
D. (2) dan (3)
E. (3)
Pembahasan:
Perhatikan persamaan-persamaan berikut yang berlaku pada kecepatan linear (v) dan kecepatan anguler/kecepatan sudut (ω) berikut.
- ω = 2πf → kecepatan sudut sebanding dengan frekuensi
- ω = 2π/T → kecepatan sudut berbanding terbalik dengan periode
- v = 2πrf
v = ωr → kecepatan linear sebanding dengan kecepatan sudut
Jadi jawaban yang sesuai adalah nomor (1) dan (2).
Jawaban: B
Contoh 2 – Soal Kecepatan Tangensial (Pengguaan Rumus Linear dan Anguler pada Gerak Melingkar)
Sebuah roda yang berjari-jari 50 cm berotasi dengan kecepatan sudut 900 rpm. Kelajuan tangensial sebuah titik pada tepi roda itu adalah ….
A. 7,5π m/s
B. 15π m/s
C. 225π m/s
D. 350π m/s
E. 450π m/s
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Jari-jari roda: r = 50 cm = 0,5 cm
- Kecepatan sudut: ω = 900 rpm
Menyatakan satuan kecepatan sudut dalam rad/s:
ω = 900 rpm
ω = 900 × 2π/60 rad/s = 30π rad/s
Menghitung kelajuan tangensial sebuah titik pada tepi roda:
v = ωr
= 30π × 0,5
= 15π m/s
Jadi, kelajuan tangensial sebuah titik pada tepi roda itu adalah 15π m/s.
Jawaban: B
Contoh 3 – Soal Penerapan Rumus Kecepatan Linear dan Anguler pada Gerak Melingkar
Sebuah roda yang berjari-jari 50 cm berputar dengan kelajuan sudut sebesar 100 rad/s. Kelajuan berubah menjadi 60 rad/s dalam waktu 10 s. Roda akan berhenti pada setelah ….
A. 5 detik
B. 10 detik
C. 15 detik
D. 20 detik
E. 25 detik
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Jari-jari roda: r = 50 cm = 0,5 m
- Kelajuan sudut awal: ω0 = 100 rad/s
- Kelajuan sudut saat waktu 10 s (t = 10 s): ω10 = 60 rad/s
Kelajuan linear saat t = 0 s:
v0 = ω0 × r
= 100 × 0,5
= 50 m
Kelajuan linear saat t = 10 s:
v10 = ω10 × r
= 60 × 0,5
= 30 m
Menghitung percepatan yang dialami benda:
vt = v0 + at
30 = 50 + a(10)
10a = 30 – 50
10a = –20
a = –20/10 = –2 m/s2
Menentukan waktu kapan roda akan berhenti vt = 0:
vt = v0 + at
0 = 50 + (–2)t
2t = 50
t = 50/2 = 25 sekon
Jadi, roda akan berhenti pada setelah 25 detik.
Jawaban: E
Demikianlah tadi ulasan materi kecepatan linear dan anguler pada gerak melingkar. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menghitung Resultan Vektor 3 Arah Secara Analitis
Sumber gini.com



EmoticonEmoticon