Turunan Hasil Kali dan Hasil Bagi Dua Fungsi

Turunan adalah permasalah yang berawal dari mencari kemiringan garis singgung pada suatu kurva. Besar kemiringan garis singgung dapat ditentukan dengan pendekatan limit. Selanjutnya, persamaan pendekatan tersebut dinyatakan dalam definisi turunan. Melalui definisi turunan dapat diperoleh berbagai aturan untuk mengetahui turunan berbagai bentuk fungsi, termasuk turunan hasil kali dan hasil bagi dua fungsi.

Definisi turunan menjadi dasar untuk mendapatkan suatu fungsi baru yang merupakan turunan fungsi. Persamaan dalam definisi turunan menyatakan nilai yang didekati dengan limit suatu nilai. Cara mencari turunan hasil kali dan hasil bagi turunan juga dilakukan melalui definisi turunan. Sayangnya, cara menentukan bentuk turunan fungsi dengan definisi turunan memiliki langkah yang sangat panjang. Sehingga diperlukan metode lain yang lebih praktis pada fungsi yang rumit seperti perkalian dan pembagian dua fungsi.

Cara untuk menentukan turunan hasil kali dan hasil bagi dua fungsi termuat dalam aturan hasil kali dan aturan hasil bagi. Bagaimana, cara menentukan turunan hasil kali dan hasil bagi dua fungsi? Sobat idschool dapat mencari tahu lebih banyak melalui ulasan di bawah.

Baca Juga: Pengertian Turunan Suatu Fungsi

Aturan Hasil Kali pada Turunan

Aturan hasil kali pada turunan akan sangat membantu untuk menentukan turunan dari fungsi dengan bentuk cukup rumit. Contoh fungsi yang dapat ditentukan turunannya dengan aturan hasil kali adalah fungsi-fungsi seperti daftar berikut.

• B(x) = (3x² + 1)⁵(x – 1)
• g(x) = 2x⁵(3x² + 1)²
• y = (x + 6)(3x² + 1)⁶
• p(x) = 2x⁵(3x² + 1)²
• f(x) = (2x² – 5)(x² + 2)!

Turunan dari sebuah fungsi yang memuat dua fungsi dapat dilakukan dengan mengalikannya terlebih dahulu. Misalnya pada contoh di bawah, mencari turunan f(x) = (2x² – 5)(x² + 2).

f(x) = (2x² – 5)(x² + 2)
= 2x⁴ + 4x² – 5x² – 10
= 2x⁴ – x² – 10

Sehingga turunan fungsi f(x) dapat secara mudah diperoleh.

f(x) = 2x⁴ – x² – 10
f’(x) = 8x⁴ – 2x

Namun cara tersebut tidak akan berguna dengan baik pada bentuk fungsi yang lebih kompleks seperti B(x) = (3x² + 1)⁵(x – 1). Hasil kali fungsi B(x) mempunyai proses yang sangat panjang dan tidak menguntungkan. Sehingga diperlukan cara lain untuk mendapatkan turunannnya. Turunan seperti pada fungsi B(x) = (3x² + 1)⁵(x – 1) akan lebih dicari dengan aturan hasil kali.

Bukti:

• andaikan F(x) = f(x) · g(x)
• turunan pertama f(x) = f’(x)
• turunan pertama g(x) = g’(x)

Turunan pertama fungsi F(x) atau F’(x):

Selanjutnya, coba lihat penggunaan aturan hasil kali untuk menentukan turunan fungsi seperti di atas.

Contoh: Tentukan turunan pertama dari f(x) = (2x² – 5)(x² + 2)!

Langkah-langkah menentukan turunan fungsi f(x) = (2x² – 5)(x² + 2) dengan aturan hasil kali.

1. Memisakan dua buah fungsi dalam u dan v, serta mencari turunan masing-masing.

Misalkan:

• u = 2x² – 5 → du = 4x dx
• v = x² + 2 → dv = 2x dx

2. Mencari turunan pertama fungsi f(x):
f’(x) = (2x² – 5)(2x) + 4x(x² + 2)
f’(x) = 4x³ – 10x + 4x³ + 8x
= 4x³ + 4x³ – 10x + 8x
= 8x³ – 2x

Diperoleh hasil turunan yang sama dengan cara sebelumnya yaitu f’(x) = 8x³ – 2x.

Baca Juga: Turunan Fungsi Trigonometri

Aturan Hasil Bagi pada Turunan

Aturan hasil bagi memiliki tujuan penggunaan yang sama dengan bahasan sebelumnya. Persamaan umum yang terdapat pada aturan hasil bagi juga berasal dari definisi turunan. Sehingga, aturan hasil bagi dapat dibuktikan kebenarannya. Persamaan yang dapat digunakan untuk mencari hasil bagi dua fungsi adalah sebagai berikut.

Bukti:

• andaikan F(x) = ^f(x)/_g(x)
• turunan pertama f(x) = f’(x)
• turunan pertama g(x) = g’(x)

Turunan pertama fungsi F(x) atau F’(x):

Contoh: Tentukan turunan pertama dari fungsi f(x) seperti persamaan berikut!

Proses mendapatkan turunan pertama fungsi f(x).

Misalkan:

• u = x² – 1 → du = 2x dx
• v = x + 1 → dv = 1 dx

Mencari turunan pertama f(x):

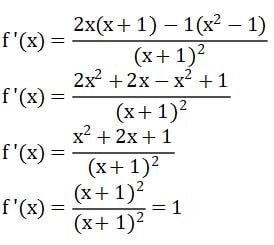
Sehingga diperoleh hasil turunan pertama untuk fungsi f(x) adalah f’(x) = 1.

Penggunaan kedua aturan (hasil kali dan hasil bagi) tersebut untuk sangat memebantu untuk bentuk yang lebih kompleks dan rumit. Cara menggunakan aturan hasil kali dan hasil bagi untuk menyelesaikan soal dapat dilihat melalui contoh soal dan pembahasan berikut.

Baca Juga: Aplikasi Turunan – Mencari Luas Maksimum/Minumum Suatu Daerah

Contoh Soal dan Pembahasan

Beberapa contoh soal turunan fungsi berikut dapat diselesaikan dengan aturan hasil kali dan hasil bagi pada turunan. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Berhasil menyelesaikan soal dengan baik dapat menjadi indikator memahami materi dengan baik. Selamat berlatih!

Contoh 1 – Soal Turunan Pertama Hasli Kali Dua Fungsi

Turunan pertama dari fungsi f(x) = 3x²(2x – 5)⁶ adalah f’(x) = ….
A. (40x² – 30x)(2x – 5)⁶
B. 6x(8x – 5)(2x – 5)⁵
C. 6x(8x – 5)(2x – 5)⁶
D. 12x(8x – 5)(2x – 5)⁵
E. 12x(8x – 5)(2x – 5)⁶

Pembahasan:

Misalkan:

• u = 3x² → du = 6x dx
• v =(2x – 5)⁶ → dv = 6(2x – 5)⁵ · 2 dx = 12(2x – 5)⁵ dx

Mencari turunan pertama dari fungsi f(x) = 3x²(2x – 5)⁶:

f’(x) = 6x · (2x – 5)⁶ + 12(2x – 5)⁵ · 3x²
f’(x) = 6x · (2x – 5)(2x – 5)⁵ + 36x²(2x – 5)⁵
= (12x² – 30x + 36x²)(2x – 5)⁵
= (48x² – 30x)(2x – 5)⁵ = 6x(8x – 5)(2x – 5)⁵

Jadi, turunan pertama dari fungsi f(x) = 3x²(2x – 5)⁶ adalah f’(x) = 6x(8x – 5)(2x – 5)⁵.

Jawaban: B

Contoh 2 – Soal Turunan Pertama Hasil Bagi Dua Fungsi

Pembahasan:

Misalkan:

• u = x² + 4 → du = 2x dx
• v = √x → dv = ¹/_2√x

Mencari turunan pertama fungsi f(x):

Jawaban: A

Demikianlah tadi ulasan cara mencari turunan hasil kali dan hasil bagi dua fungsi. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Aplikasi Turunan untuk Menghitung Biaya Produksi Minimum

Sumber gini.com